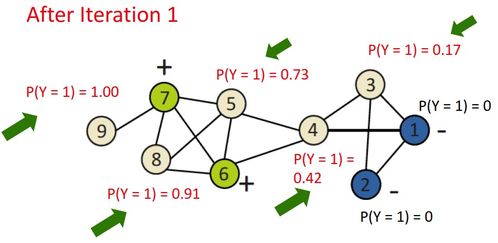
图神经网络(GNN)的核心思想之一是通过信息传播(Message Passing) 机制来学习节点表示,并进而完成节点分类等任务。本讲重点探讨如何利用图中节点间的连接关系(即“法图信息”,或更准确地称为“图结构信息”)来对未标记节点进行半监督分类。
1. 问题定义:半监督节点分类
在许多现实图数据(如社交网络、引用网络)中,仅有部分节点拥有标签(如用户的兴趣类别、论文的研究领域)。目标是利用这些少量标签以及丰富的图结构(连接关系),预测未标记节点的类别。这属于典型的半监督学习场景。
关键假设:同质性(Homophily)。即相连的节点倾向于具有相似的属性或标签。“物以类聚,人以群分”是图数据中普遍存在的规律,这构成了信息传播的理论基础。
2. 核心思想:基于集体分类的迭代算法
传统方法不依赖节点特征,仅利用图结构和已知标签。基本框架是迭代式的集体分类(Collective Classification),包含三个主要步骤:
1. 局部分类器(Local Classifier):初始时,仅使用节点自身的属性(如果有)或给予未标记节点一个初始预测。
2. 关系分类器(Relational Classifier):利用邻居节点的标签或预测结果来更新当前节点的预测。其核心公式常表示为:
\[ P(Yi = c) = \frac{1}{\mathcal{N}(i)} \sum{j \in \mathcal{N}(i)} P(Y_j = c) \]
即,节点 \(i\) 属于类别 \(c\) 的概率是其所有邻居 \(j\) 属于该类别概率的平均。这直接体现了“邻居影响我”的思想。
- 集体推理(Collective Inference):迭代执行步骤2,让标签信息在整个图中传播,直至收敛或达到迭代次数。常用方法包括迭代分类、信念传播等。
3. 典型算法:标签传播
标签传播算法(Label Propagation) 是上述思想的经典实现。
- 初始化:将所有已标记节点的标签固定,未标记节点赋予一个统一的随机分布或均匀分布。
- 迭代更新:每个节点将其标签分布更新为其所有邻居节点标签分布的加权平均。对于未标记节点:
\[ \mathbf{Y}i^{(t+1)} = \sum{j \in \mathcal{N}(i)} \frac{1}{\deg(i)} \mathbf{Y}j^{(t)} \]
其中 \(\mathbf{Y}i\) 是节点 \(i\) 的标签概率向量。
- 收敛:重复迭代直到标签分布变化很小或达到最大迭代次数。未标记节点的标签取其概率最大的类别。
该算法的核心是创建一个“标签流”从已标记节点通过边向未标记节点扩散的过程。
4. 与图神经网络的联系
现代图神经网络(如GCN)本质上是带参数、多层次、结合节点特征的信息传播框架。
- GNN中的消息传递(Message Passing) 可以看作上述标签传播的可微、参数化、特征增强的扩展。
- 每一层,节点聚合来自其邻居的消息(经过变换的特征),并结合自身信息更新其表示。
- 通过堆叠多层,信息可以传播到多跳邻居,捕获更广泛的图结构上下文。
- 基于学习到的节点表示(而非直接的标签分布)进行分类预测。
因此,传统基于图结构的标签传播算法可以视为一个简单的、无参数、无特征的“单层GNN”。它验证了纯粹利用图结构进行半监督学习的可行性,并为GNN的设计提供了直观的动机。
5.
信息传播与节点分类紧密相连。传统方法(如标签传播)直接利用图结构的同质性假设,通过迭代平均邻居标签来推断未知节点类别。这些方法虽然简单,但清晰地展示了图结构本身蕴含的强大预测信号。现代图神经网络继承了这一核心思想,但通过可学习的非线性变换、节点特征融合以及深度架构,极大地增强了模型的表达能力和适用性,成为处理图数据半监督学习任务的主流工具。理解这一演进脉络,有助于我们更深刻地把握GNN的设计原理与优势。